
損益分岐点分析をマスターする~実践編~
今回は損益分岐点分析の実践編となります。(参考:損益分岐点分析をマスターする!~基礎編~)実践編では、最小二乗法という費用を統計的に固定費と変動費に分類する方法を用いて、各社の損益分岐点をみていきます。
Microsoft Office Excelを使用して、グラフを作成する方法をご紹介します。売上高をX軸・総費用をY軸とした散布図です。今回は売上高を3カ年分の四半期データ(データ数:12)としました。総費用は売上原価と販管費を合計したものですが、今回は売上高から営業利益を差し引いて算出しています。
散布図を作成したら、プロットされたデータの近似曲線を追加します。グラフ上の任意の一点上で右クリックをして、ショートカットメニューを表示させ、「近似曲線の追加」を選択します。
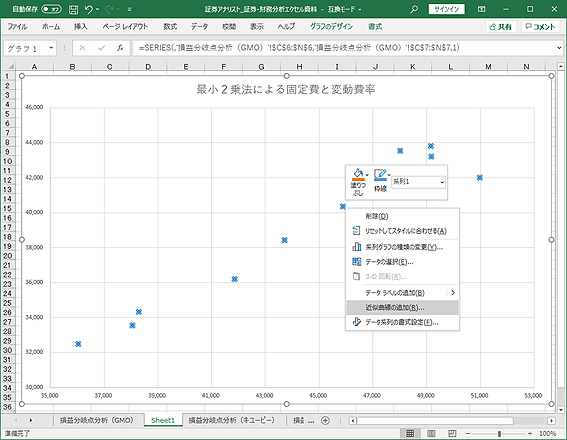
そして、近似曲線のオプションで、「グラフに数式を表示する」「グラフにR-2乗値を表示する」のチェックボックスをオンにします。
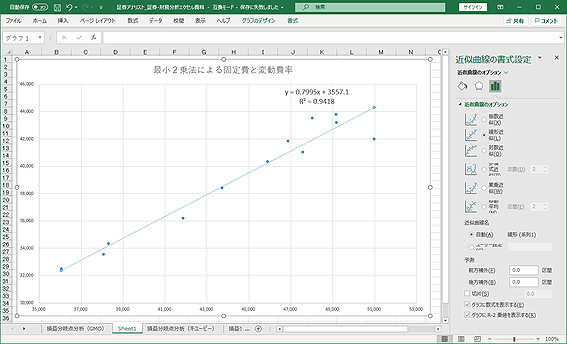
するとy = 0.7995x + 3557 R2 = 0.9418 R2 = 0.9418がグラフに表示されます。y=ax+bのa(0.7995)が変動費率、b( 3557 )が固定費です。そして、R2が決定係数となります。なお、この数式と決定係数はこの後に出てくるGMOインターネットの計算結果です。
GMOインターネットの2017年度~2019年度までの3カ年の四半期データ(データ数12:同社データシートより四半期売上高と営業利益のデータ取得)を使用し、最小二乗法で損益分岐点を計算した結果は以下となります。
y = 0.7995x + 3557 R2 = 0.9418
| 固定費(百万円) | 3,557 |
|---|---|
| 変動費率 | 0.7995 |
| 限界利益率(=1-変動費率) | 0.2005 |
損益分岐点売上高=固定費÷限界利益率(=1-変動費率)
損益分岐点売上高=35億5700万円÷0.2005=177億4100万円
同社の19.12期4Qの売上高は491億5700万円ですので、以下の公式にあてはめると、
損益分岐点比率=損益分岐点売上高÷実際の売上高×100
損益分岐点比率=177億4100万円÷491億5700万円×100=36.1% となります。このように、GMOインターネットは売上高が64%減少しない限り赤字にはならないとここでは計算されました。
GMOインターネットは損益分岐点比率が低いですので、多少売上高が減少しても赤字にならないと考えることができます。また、最小二乗法における計算での決定係数(R2)は0.94でした。決定係数は1に近いほど結果の信頼性が高いといえますので、今回算出した数値の信頼性は高いといえます。
キユーピーの2017年度~2019年度までの3カ年の四半期データ(データ数12:同社ウェブサイトより四半期売上高と営業利益のデータ取得)を使用し、最小二乗法で損益分岐点を計算した結果は以下となります。
y = 0.7478x + 27303 R2 = 0.9455
| 固定費(百万円) | 27,303 |
|---|---|
| 変動費率 | 0.7478 |
| 限界利益率(=1-変動費率) | 0.2522 |
損益分岐点売上高=固定費÷限界利益率(=1-変動費率)
損益分岐点売上高=273億0300万円÷0.2522=1082億5900万円
同社の19.11期4Qの売上高は1382億5600万円ですので、以下の公式にあてはめると、
損益分岐点比率=損益分岐点売上高÷実際の売上高×100
損益分岐点比率=1082億5900万円÷1382億5600万円×100=78.3% となります。このようにキユーピーは売上高が22%超減少すれば赤字になるとここでは計算されました。
キユーピーは、損益分岐点比率が低いといえませんので、売上高が大きく減少した場合は赤字に転落する可能性があります。なお、最小二乗法における計算での決定係数(R2)は0.95だったので、今回算出した数値の信頼性は高いといえます。
オリンパスの2017年度~2019年度までの3カ年の四半期データ(データ数12:同社決算参考資料より四半期売上高と営業利益のデータ取得)を使用し、最小二乗法で損益分岐点を計算した結果は以下となります。
y = 0.5843x + 66308 R2 = 0.3338
| 固定費(百万円) | 66,308 |
|---|---|
| 変動費率 | 0.5843 |
| 限界利益率(=1-変動費率) | 0.4157 |
損益分岐点売上高=固定費÷限界利益率(=1-変動費率)
損益分岐点売上高=663億0800万円÷0.4157=1595億0900万円
同社の20.3期4Qの売上高は2023億4000万円ですので、以下の公式にあてはめると、
損益分岐点比率=損益分岐点売上高÷実際の売上高×100
損益分岐点比率=1595億0900万円÷2023億4000万円×100=78.8% となります。このようにオリンパスは売上高が21%減少すれば赤字になるとここでは計算されました。
オリンパスは、損益分岐点比率が高いですので、売上高が大きく減少した場合は赤字に転落する可能性があります。ただし、今回の計算での決定係数(R2)は0.33でしたので、信頼性は高いとはいえません。決定係数が低い場合の結果はあてになりませんので、決定係数を高めるための対応(データ数の変更など)を行う必要があります。
最小二乗法を用いた損益分岐点の計算において必要となるデータは、売上高と営業利益のみです。「必要となるデータ数が少ない」、これが最小二乗法の最大のメリットといえます。
今回は3カ年の四半期データ(データ数:12)を使用しましたが、特に決まりはありません。大事なことはデータ数ではなく、結果として出てくる決定係数が高いかどうかです。個人的には四半期で、2~3カ年分のデータを使用するのがよいかと思います。あまり長い期間で集計するとその会社の費用構造が途中で変化している可能性があります。そうなると決定係数は低くなります。
また、国際会計基準(IFRS)を適用している会社の営業利益は、日本基準の営業費用や特別損失の影響を受けることとなりますので、営業利益のブレが大きくなり、決定係数は低くなりやすいといえます。今回計算したオリンパスの決定係数が低く出たのは、同社がIFRSを適用していることも要因であると考えられます。
最後に、損益分岐点分析はファンダメンタル分析のなかでも非常に有用です。最小二乗法は簡易的に損益分岐点を計算することができるので、使い勝手がよいといえます。ぜひ使いこなして自身の銘柄選定などに役立ててください。

